从数学角度来看,最优化方法是一种求极值的方法,即在一组约束为等式或不等式的条件下,使系统的目标函数达到极值,即最大值或最小值。从工程角度,最优控制是在可行条件下寻求最佳控制策略,以使控制系统能够最优地到达目标。
最优控制策略的构建离不开对机器人的建模。只有充分分析机器人的物理模型,才能更好地理解机器人系统的性能,以及如何优化机器人控制器的设计系统。
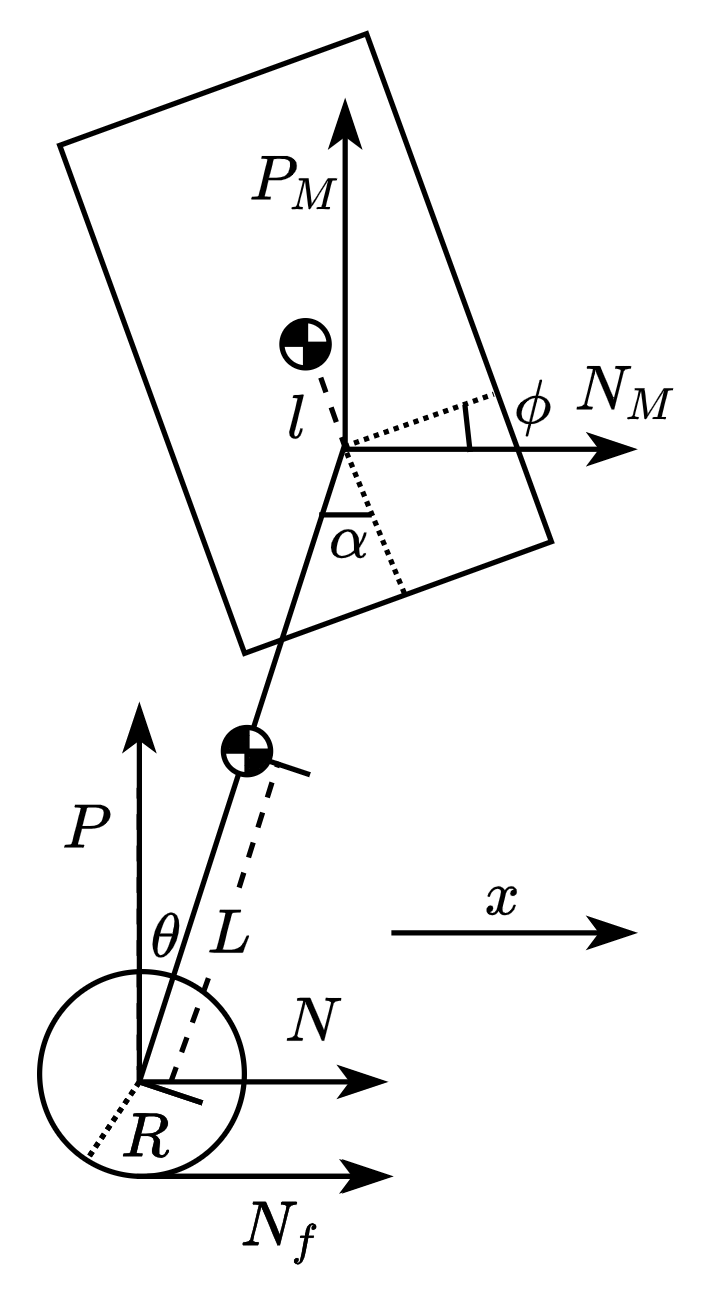
对于轮足机器人的平衡与纵向运动控制,主要关注机器人机体姿态、腿部姿态和驱动轮的运动。称机器人中机体与腿部机构转轴、腿部机构与驱动轮轴之间的连线为摆杆,得到如图1所示的轮足倒立摆模型,模型中变量与参数的定义如表1和表2所示。
图1. 轮足倒立摆模型
表1. 轮足倒立摆模型变量定义
符号 含义 正方向 单位 θ \theta θ 摆杆与竖直方向夹角 图示为正方向 rad α \alpha α 摆杆与机体相对角度 同θ \theta θ rad ϕ \phi ϕ 机体与水平夹角 图示为正方向 rad x c x_c x c 驱动轮位移 箭头所示 m x x x 膝部结构转轴位移 同x c x_c x c m T T T 驱动轮输出力矩 同θ \theta θ Nm T p T_p T p 膝关节输出力矩 同α \alpha α Nm N N N 驱动轮对摆杆力的水平分量 箭头所示 N P P P 驱动轮对摆杆力的竖直分量 箭头所示 N N f N_f N f 地面对驱动轮的摩擦力 箭头所示 N N M N_M N M 摆杆对机体水平方向分量 箭头所示 N P M P_M P M 摆杆对机体竖直方向分量 箭头所示 N F F F 摆杆推力 向外为正 N
表2. 轮足倒立摆模型参数定义
符号 单位 含义 R R R m 驱动轮半径 L L L m 摆杆重心到驱动轮轴距离 L M L_M L M m 摆杆重心到机体转轴距离 l l l m 机体重心到其转轴距离 m w m_w m w kg 驱动轮转子质量 m p m_p m p kg 摆杆质量 M M M kg 机体质量 I w I_w I w Kg·m² 驱动轮转子转动惯量 I p I_p I p Kg·m² 摆杆质量转动惯量 I M I_M I M Kg·m² 机体绕转轴转动惯量
对驱动轮分析,有:
m w x ¨ = N f − N \begin{equation}
{m_w}\ddot x = {N_f} - N
\end{equation} m w x ¨ = N f − N I w x ¨ R = T − N f R \begin{equation}
{I_w}\frac{{\ddot x}}{R} = T - {N_f}R
\end{equation} I w R x ¨ = T − N f R 消去 N f N_f N f
x ¨ = T − N R I w R + m w R \begin{equation}
\ddot x = \frac{{T - NR}}{{\frac{{{I_w}}}{R} + {m_w}R}}
\end{equation} x ¨ = R I w + m w R T − NR 针对摆杆进行分析,有:
N − N M = m p ∂ 2 ∂ t 2 ( x + L sin θ ) \begin{equation}
N - {N_M} = {m_p}\frac{{{\partial ^2}}}{{\partial {t^2}}}(x + L\sin \theta )
\end{equation} N − N M = m p ∂ t 2 ∂ 2 ( x + L sin θ ) P − P M − m p g = m p ∂ 2 ∂ t 2 ( L cos θ ) \begin{equation}
P - {P_M} - {m_p}g = {m_p}\frac{{{\partial ^2}}}{{\partial {t^2}}}(L\cos \theta )
\end{equation} P − P M − m p g = m p ∂ t 2 ∂ 2 ( L cos θ ) I p θ ¨ = ( P L + P M L M ) sin θ − ( N L + N M L M ) cos θ − T + T p \begin{equation}
{I_p}\ddot \theta = \left( {PL + {P_M}{L_M}} \right)\sin \theta - \left( {NL + {N_M}{L_M}} \right)\cos \theta - T + {T_p}
\end{equation} I p θ ¨ = ( P L + P M L M ) sin θ − ( N L + N M L M ) cos θ − T + T p 对机体进行分析,有:
N M = M ∂ 2 ∂ t 2 ( x + ( L + L M ) sin θ − l sin ϕ ) \begin{equation}
{N_M} = M\frac{{{\partial ^2}}}{{\partial {t^2}}}\left( {x + \left( {L + {L_M}} \right)\sin \theta - l\sin \phi } \right)
\end{equation} N M = M ∂ t 2 ∂ 2 ( x + ( L + L M ) sin θ − l sin ϕ ) P M − M g = M ∂ 2 ∂ t 2 ( ( L + L M ) cos θ + l cos ϕ ) \begin{equation}
{P_M} - Mg = M\frac{{{\partial ^2}}}{{\partial {t^2}}}\left( {\left( {L + {L_M}} \right)\cos \theta + l\cos \phi } \right)
\end{equation} P M − M g = M ∂ t 2 ∂ 2 ( ( L + L M ) cos θ + l cos ϕ ) I M ϕ ¨ = T p + N M l cos ϕ + P M l sin ϕ \begin{equation}
{I_M}\ddot \phi = {T_p} + {N_M}l\cos \phi + {P_M}l\sin \phi
\end{equation} I M ϕ ¨ = T p + N M l cos ϕ + P M l sin ϕ 定义状态空间模型中的状态向量 x \textbf{x} x
x = [ θ θ ˙ x x ˙ ϕ ϕ ˙ ] \textbf{x} = {\begin{bmatrix}
\theta \\
{\dot \theta }\\
x\\
{\dot x}\\
\phi \\
{\dot \phi }
\end{bmatrix}} x = θ θ ˙ x x ˙ ϕ ϕ ˙ 控制向量 u \textbf{u} u
u = [ T T p ] \textbf{u} = {\begin{bmatrix}
T\\
{{T_p}}
\end{bmatrix}} u = [ T T p ] 定义系统的非线性模型:
x ˙ = f ( x , u ) \dot{\textbf{x}} = f(\textbf{x},\textbf{u}) x ˙ = f ( x , u ) 由式(3) ~ (9),可以得到系统非线性模型的符号表达式。根据状态向量和控制向量,在非线性模型的平衡点处使用雅可比矩阵线性化,可以得到:
A = ∂ f ∂ x ( x ˉ , u ˉ ) , B = ∂ f ∂ u ( x ˉ , u ˉ ) A = \frac{{\partial f}}{{\partial {\textbf{x}}}}(\bar {\textbf{x}},\bar {\textbf{u}}),B = \frac{{\partial f}}{{\partial {\textbf{u}}}}(\bar {\textbf{x}},\bar {\textbf{u}}) A = ∂ x ∂ f ( x ˉ , u ˉ ) , B = ∂ u ∂ f ( x ˉ , u ˉ ) 其中 x ˉ , u ˉ \bar {\textbf{x}},\bar {\textbf{u}} x ˉ , u ˉ f ( x ˉ , u ˉ ) = 0 f\left(\bar {\textbf{x}},\bar {\textbf{u}}\right)=0 f ( x ˉ , u ˉ ) = 0
x ˉ = [ 0 0 x 0 0 0 ] , u ˉ = [ 0 0 ] \bar x = {\begin{bmatrix}
0\\
0\\
x\\
0\\
0\\
0
\end{bmatrix}},\bar u = {\begin{bmatrix}
0\\
0
\end{bmatrix}} x ˉ = 0 0 x 0 0 0 , u ˉ = [ 0 0 ] 有:
x ˙ = [ 0 1 0 0 0 0 A 1 0 0 0 A 2 0 0 0 0 1 0 0 A 3 0 0 0 A 4 0 0 0 0 0 0 1 A 5 0 0 0 A 6 0 ] x + [ 0 0 B 1 B 2 0 0 B 3 B 4 0 0 B 5 B 6 ] u \dot {\textbf{x}} = {\begin{bmatrix}
0&1&0&0&0&0\\
{{A_1}}&0&0&0&{{A_2}}&0\\
0&0&0&1&0&0\\
{{A_3}}&0&0&0&{{A_4}}&0\\
0&0&0&0&0&1\\
{{A_5}}&0&0&0&{{A_6}}&0
\end{bmatrix}} \textbf{x} + {\begin{bmatrix}
0&0\\
{{B_1}}&{{B_2}}\\
0&0\\
{{B_3}}&{{B_4}}\\
0&0\\
{{B_5}}&{{B_6}}
\end{bmatrix}}\textbf{u} x ˙ = 0 A 1 0 A 3 0 A 5 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 A 2 0 A 4 0 A 6 0 0 0 0 1 0 x + 0 B 1 0 B 3 0 B 5 0 B 2 0 B 4 0 B 6 u 所有的状态变量均可以通过数据融合解算或测量得到结果,此时系统输出 y \textbf{y} y
y = I 6 x \textbf{y} = {I_6}\textbf{x} y = I 6 x 其中,I 6 {I_6} I 6 A A A B B B
根据上文建立的轮足机器人的系统模型,设计控制律为系统状态的线性组合,则:
u = − K x = − [ K 11 K 12 K 13 K 14 K 15 K 16 K 21 K 22 K 23 K 24 K 25 K 26 ] [ θ ˙ θ ˙ x x ˙ ϕ ϕ ˙ ] \textbf{u} = - K\textbf{x} = - {\begin{bmatrix}
{{K_{11}}}&{{K_{12}}}&{{K_{13}}}&{{K_{14}}}&{{K_{15}}}&{{K_{16}}}\\
{{K_{21}}}&{{K_{22}}}&{{K_{23}}}&{{K_{24}}}&{{K_{25}}}&{{K_{26}}}
\end{bmatrix}} {\begin{bmatrix}
{\dot \theta }\\
{\dot \theta }\\
x\\
{\dot x}\\
\phi \\
{\dot \phi }
\end{bmatrix}} u = − K x = − [ K 11 K 21 K 12 K 22 K 13 K 23 K 14 K 24 K 15 K 25 K 16 K 26 ] θ ˙ θ ˙ x x ˙ ϕ ϕ ˙ 使用线性二次型调节器(LQR)计算增益矩阵 K K K J J J
J = ∫ 0 ∞ ( x T Q x + u T R u ) d t J = \int_0^\infty {\left( {{x^T}\textbf{Q}x + {u^T}\textbf{R}u} \right)} {\rm{ d}}t J = ∫ 0 ∞ ( x T Q x + u T R u ) d t 为了使代价函数具有最小值,则输入 u \textbf{u} u
u = − R − 1 B T Px \textbf{u} = - \textbf{R}^{-1} \textbf{B}^T \textbf{Px} u = − R − 1 B T Px 即增益矩阵 K \textbf{K} K
K = R − 1 B T P \textbf{K} = \textbf{R}^{-1} \textbf{B}^T \textbf P K = R − 1 B T P 其中P满足代数黎卡提方程:
A T P + PA − PB R − 1 B T P + Q = 0 \textbf{A}^T \textbf P + \textbf P \textbf A - \textbf P \textbf B \textbf{R}^{ - 1} \textbf{B}^T \textbf P + \textbf Q = 0 A T P + P A − P B R − 1 B T P + Q = 0 通过上述方法可以使系统在线性化平衡点附近稳定,为了使机器人具备跟踪轨迹的功能,还需要在系统输入中加入参考输入,即:
u = K ( x d − x ) \textbf u = \textbf {K} (\textbf{x}d - \textbf x) u = K ( x d − x ) 其中 x d \textbf{x}_d x d x ~ \tilde {\textbf{x}} x ~
x d = [ 0 0 x ~ 0 0 0 ] \textbf{x}_d = {\begin{bmatrix}
0\\
0\\
\tilde {\textbf{x}}\\
0\\
0\\
0
\end{bmatrix}} x d = 0 0 x ~ 0 0 0 在建立轮足机器人的物理模型时,没有考虑到腿长的变化对系统带来的影响。因此为了考虑在不同腿长下的工况,定义一定的腿长区间,在腿长区间内每隔10mm对系统模型进行一次线性化,并求解LQR的增益矩阵 K \textbf{K} K K i j \textbf{K}_{ij} K ij L 0 = L + L M L_0=L+L_M L 0 = L + L M
K i j ( L 0 ) = p 0 ∣ i j + p 1 ∣ i j L 0 + p 2 ∣ i j L 0 2 + p 3 ∣ i j L 0 3 {K_{ij}}\left( {{L_0}} \right) = {p_{0|ij}} + {p_{1|ij}}{L_0} + {p_{2|ij}}L_0^2 + {p_{3|ij}}L_0^3 K ij ( L 0 ) = p 0∣ ij + p 1∣ ij L 0 + p 2∣ ij L 0 2 + p 3∣ ij L 0 3 综上所述,机器人的纵向运动控制律为:
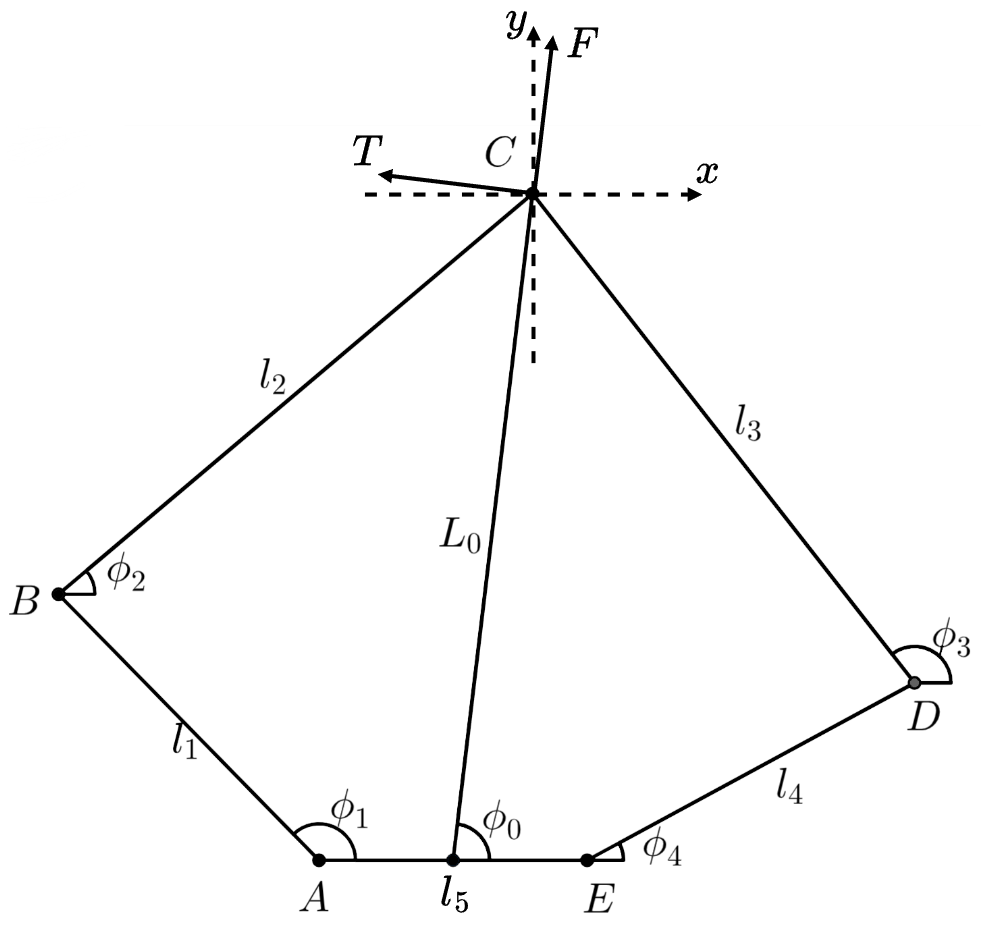
u = K ( L 0 ) ( x d − x ) \textbf u = \textbf K ({L_0})(\textbf{x}_d - \textbf x) u = K ( L 0 ) ( x d − x ) 图2. 五连杆机构参数定义图
五连杆机构参数定义如图所示,其中 A A A E E E ϕ 1 \phi_1 ϕ 1 ϕ 4 \phi_4 ϕ 4 ( x , y ) (x,y) ( x , y ) ( L 0 , ϕ 0 ) (L_0,\phi_0) ( L 0 , ϕ 0 )
{ x B + l 2 cos ϕ 2 = x D + l 3 cos ϕ 3 y B + l 2 sin ϕ 2 = y D + l 3 sin ϕ 3 \left\{ \begin{array}{l}
{x_B} + {l_2}\cos {\phi _2} = {x_D} + {l_3}\cos {\phi _3}\\
{y_B} + {l_2}\sin {\phi _2} = {y_D} + {l_3}\sin {\phi _3}
\end{array} \right. { x B + l 2 cos ϕ 2 = x D + l 3 cos ϕ 3 y B + l 2 sin ϕ 2 = y D + l 3 sin ϕ 3 求解方程组可以得到角度 ϕ 2 \phi_2 ϕ 2
ϕ 2 = 2 arctan ( B 0 + A 0 2 + B 0 2 − C 0 2 A 0 + C 0 ) {\phi _2} = 2\arctan \left( {\frac{{{B_0} + \sqrt[{}]{{A_0^2 + B_0^2 - C_0^2}}}}{{{A_0} + {C_0}}}} \right) ϕ 2 = 2 arctan ( A 0 + C 0 B 0 + A 0 2 + B 0 2 − C 0 2 ) 其中:
A 0 = 2 l 2 ( x D − x B ) B 0 = 2 l 2 ( y D − y B ) C 0 = l 2 2 + l B D 2 − l 3 2 l B D = ( x D − x B ) 2 + ( y D − y B ) 2 \begin{array}{l}
{A_0} = 2{l_2}({x_D} - {x_B})\\
{B_0} = 2{l_2}({y_D} - {y_B})\\
{C_0} = l_2^2 + l_{BD}^2 - l_3^2\\
{l_{BD}} = \sqrt {{{({x_D} - {x_B})}^2} + {{({y_D} - {y_B})}^2}}
\end{array} A 0 = 2 l 2 ( x D − x B ) B 0 = 2 l 2 ( y D − y B ) C 0 = l 2 2 + l B D 2 − l 3 2 l B D = ( x D − x B ) 2 + ( y D − y B ) 2 通过 ϕ 2 \phi_2 ϕ 2
{ x C = l 1 cos ϕ 1 + l 2 cos ϕ 2 y C = l 1 sin ϕ 1 + l 2 sin ϕ 2 \left\{ \begin{array}{l}
{x_C} = {l_1}\cos {\phi _1} + {l_2}\cos {\phi _2}\\
{y_C} = {l_1}\sin {\phi _1} + {l_2}\sin {\phi _2}
\end{array} \right. { x C = l 1 cos ϕ 1 + l 2 cos ϕ 2 y C = l 1 sin ϕ 1 + l 2 sin ϕ 2 进而得到极坐标:
{ L 0 = ( x C − l 5 / 2 ) 2 + y C 2 ϕ 0 = arctan y C x C − l 5 / 2 \left\{ \begin{array}{l}
{L_0} = \sqrt {{{({x_C} - {l_5}/2)}^2} + y_C^2} \\
{\phi _0} = \arctan \frac{{{y_C}}}{{{x_C} - {l_5}/2}}
\end{array} \right. { L 0 = ( x C − l 5 /2 ) 2 + y C 2 ϕ 0 = arctan x C − l 5 /2 y C VMC(Virtual model control,虚拟模型控制)是一种描述交互行为的方法,利用虚拟的机械构件产生的虚拟力来获得真实的执行器的扭矩或力,这些关节扭矩产生的效果与虚拟力的效果相同,均驱使机器人按照期望控制量运动。VMC方法是直觉控制方法中的典型代表,其特点是不需要进行机器人运动学的逆解,极大地提高了计算效率和控制效率。
在闭链五连杆问题中,我们需要获得五连杆机构末端的推力 F F F T p T_p T p A A A E E E T 1 T_1 T 1 T 2 T_2 T 2 x = [ L 0 ϕ 0 ] T \textbf{x}=\left[L_0\ \phi_0\right]^T x = [ L 0 ϕ 0 ] T q = [ ϕ 1 ϕ 4 ] T \textbf{q}=\left[\phi_1\ \phi_4\right]^T q = [ ϕ 1 ϕ 4 ] T x = f ( q ) \textbf{x}=f\left(\textbf{q}\right) x = f ( q )
{ δ L 0 = ∂ f 1 ∂ ϕ 1 δ ϕ 1 + ∂ f 1 ∂ ϕ 4 δ ϕ 4 δ ϕ 0 = ∂ f 2 ∂ ϕ 1 δ ϕ 1 + ∂ f 2 ∂ ϕ 4 δ ϕ 4 \begin{equation}
\left\{\begin{matrix}
{\delta {L_0} = \frac{{\partial {f_1}}}{{\partial {\phi _1}}}\delta {\phi _1} + \frac{{\partial {f_1}}}{{\partial {\phi _4}}}\delta {\phi _4}} \\
{\delta {\phi _0} = \frac{{\partial {f_2}}}{{\partial {\phi _1}}}\delta {\phi _1} + \frac{{\partial {f_2}}}{{\partial {\phi _4}}}\delta {\phi _4}}
\end{matrix}\right.
\end{equation} { δ L 0 = ∂ ϕ 1 ∂ f 1 δ ϕ 1 + ∂ ϕ 4 ∂ f 1 δ ϕ 4 δ ϕ 0 = ∂ ϕ 1 ∂ f 2 δ ϕ 1 + ∂ ϕ 4 ∂ f 2 δ ϕ 4 即:
δ x = [ ∂ f 1 ∂ ϕ 1 ∂ f 1 ∂ ϕ 4 ∂ f 2 ∂ ϕ 1 ∂ f 2 ∂ ϕ 4 ] δ q \begin{equation}
\delta x = {\begin{bmatrix}
{\frac{{\partial {f_1}}}{{\partial {\phi _1}}}}&{\frac{{\partial {f_1}}}{{\partial {\phi _4}}}}\\
{\frac{{\partial {f_2}}}{{\partial {\phi _1}}}}&{\frac{{\partial {f_2}}}{{\partial {\phi _4}}}}
\end{bmatrix}} \delta q
\end{equation} δ x = [ ∂ ϕ 1 ∂ f 1 ∂ ϕ 1 ∂ f 2 ∂ ϕ 4 ∂ f 1 ∂ ϕ 4 ∂ f 2 ] δ q 定义雅可比矩阵 J \textbf{J} J
J = [ ∂ f 1 ∂ ϕ 1 ∂ f 1 ∂ ϕ 4 ∂ f 2 ∂ ϕ 1 ∂ f 2 ∂ ϕ 4 ] {\bf{J}} = \ {\begin{bmatrix}
{\frac{{\partial {f_1}}}{{\partial {\phi _1}}}}&{\frac{{\partial {f_1}}}{{\partial {\phi _4}}}}\\
{\frac{{\partial {f_2}}}{{\partial {\phi _1}}}}&{\frac{{\partial {f_2}}}{{\partial {\phi _4}}}}
\end{bmatrix}} J = [ ∂ ϕ 1 ∂ f 1 ∂ ϕ 1 ∂ f 2 ∂ ϕ 4 ∂ f 1 ∂ ϕ 4 ∂ f 2 ] 有:
δ x = J δ q \begin{equation}
\delta {\textbf{x}} = \textbf J \delta {\textbf q}
\end{equation} δ x = J δ q 式(12)表示将关节速度 q ˙ \dot{\textbf{q}} q ˙ x ˙ \dot{\textbf{x}} x ˙
T T δ q + ( − F ) T δ x = 0 \begin{equation}
\textbf{T}^T \delta \textbf{q} + {( - \textbf{F})^T}\delta {\textbf{x}} = 0
\end{equation} T T δ q + ( − F ) T δ x = 0 其中 T = [ T 1 T 2 ] T \textbf{T}=\left[T_1\ T_2\right]^T T = [ T 1 T 2 ] T F = [ F T p ] T \textbf{F}=\left[F\ T_p\right]^T F = [ F T p ] T
T = J T F \begin{equation}
\textbf T = \textbf{J}^T \textbf F
\end{equation} T = J T F 即可通过正运动学模型雅可比矩阵求解关节电机的输出力矩。
但通过此种方法推导出的正运动学模型中存在大量的平方和三角函数嵌套运算,直接求解雅可比矩阵 J \textbf{J} J
F = T 2 cos ( φ 0 − φ 3 ) l 4 sin ( φ 3 − φ 4 ) − T 1 cos ( φ 0 − φ 2 ) l 1 sin ( φ 1 − φ 2 ) \begin{equation}
F = \frac{{{T_2}\cos \left( {{\varphi _0} - {\varphi _3}} \right)}}{{{l_4}\sin \left( {{\varphi _3} - {\varphi _4}} \right)}} - \frac{{{T_1}\cos \left( {{\varphi _0} - {\varphi _2}} \right)}}{{{l_1}\sin \left( {{\varphi _1} - {\varphi _2}} \right)}}
\end{equation} F = l 4 sin ( φ 3 − φ 4 ) T 2 cos ( φ 0 − φ 3 ) − l 1 sin ( φ 1 − φ 2 ) T 1 cos ( φ 0 − φ 2 ) T = L 0 ( T 1 cos ( φ 0 − φ 2 ) l 1 sin ( φ 1 − φ 2 ) − T 2 sin ( φ 0 − φ 3 ) l 4 sin ( φ 3 − φ 4 ) ) \begin{equation}
T = {L_0}\left( {\frac{{{T_1}\cos \left( {{\varphi _0} - {\varphi _2}} \right)}}{{{l_1}\sin \left( {{\varphi _1} - {\varphi _2}} \right)}} - \frac{{{T_2}\sin \left( {{\varphi _0} - {\varphi _3}} \right)}}{{{l_4}\sin \left( {{\varphi _3} - {\varphi _4}} \right)}}} \right)
\end{equation} T = L 0 ( l 1 sin ( φ 1 − φ 2 ) T 1 cos ( φ 0 − φ 2 ) − l 4 sin ( φ 3 − φ 4 ) T 2 sin ( φ 0 − φ 3 ) ) 整理可以得到最终的关节力矩与虚拟力的映射关系:
T 1 = − L 1 sin ( φ 1 − φ 2 ) ( T cos ( φ 0 − φ 3 ) + F L 0 sin ( φ 0 − φ 3 ) L 0 sin ( φ 2 − φ 3 ) \begin{equation}
{T_1} = - \frac{{{L_1}\sin \left( {{\varphi _1} - {\varphi _2}} \right)\left( {T\cos \left( {{\varphi _0} - {\varphi _3}} \right) + F{L_0}\sin \left( {{\varphi _0} - {\varphi _3}} \right)} \right.}}{{{L_0}\sin \left( {{\varphi _2} - {\varphi _3}} \right)}}
\end{equation} T 1 = − L 0 sin ( φ 2 − φ 3 ) L 1 sin ( φ 1 − φ 2 ) ( T cos ( φ 0 − φ 3 ) + F L 0 sin ( φ 0 − φ 3 ) T 2 = − L 4 sin ( φ 3 − φ 4 ) ( T cos ( φ 0 − φ 2 ) + F L 0 sin ( φ 0 − φ 2 ) L 0 sin ( φ 2 − φ 3 ) \begin{equation}
{T_2} = - \frac{{{L_4}\sin \left( {{\varphi _3} - {\varphi _4}} \right)\left( {T\cos \left( {{\varphi _0} - {\varphi _2}} \right) + F{L_0}\sin \left( {{\varphi _0} - {\varphi _2}} \right)} \right.}}{{{L_0}\sin \left( {{\varphi _2} - {\varphi _3}} \right)}}
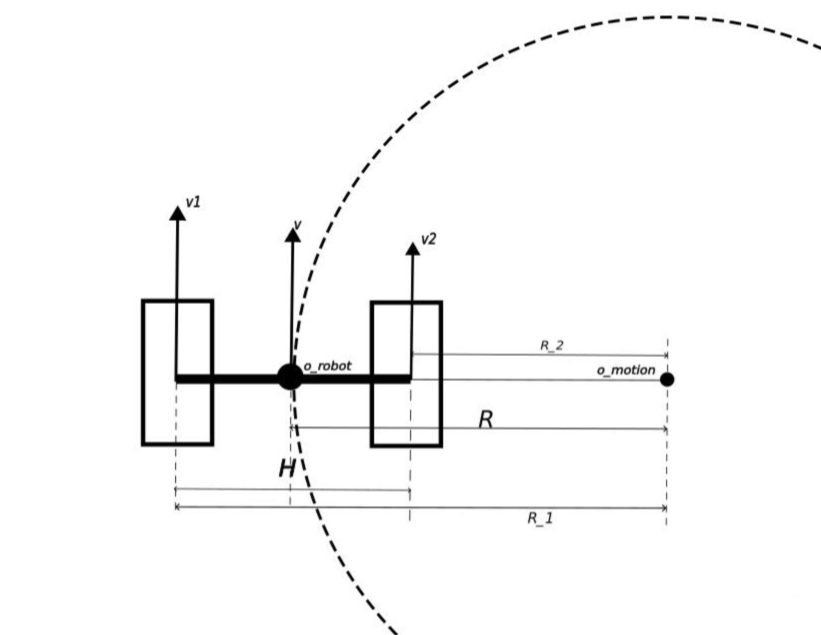
\end{equation} T 2 = − L 0 sin ( φ 2 − φ 3 ) L 4 sin ( φ 3 − φ 4 ) ( T cos ( φ 0 − φ 2 ) + F L 0 sin ( φ 0 − φ 2 ) 轮足机器人的轮式模型可以认为是两轮差速驱动运动模型(图3),由两个独立驱动的轮子驱动,图3-3中 H \textbf{H} H R \textbf{R} R v 1 = v 2 {v}_1=v_2 v 1 = v 2 v = v 1 = v 2 v=v_1=v_2 v = v 1 = v 2 v 1 ≠ v 2 v_1\ \neq v_2 v 1 = v 2
图3. 两轮差速驱动运动模型
(1) v 1 { v}_1 v 1 v 2 v_2 v 2
ω = v 2 R − H 2 = v 1 R + H 2 = v R \begin{equation}
\omega = \frac{{{v_2}}}{{R - \frac{H}{2}}} = \frac{{{v_1}}}{{R + \frac{H}{2}}} = \frac{v}{R}
\end{equation} ω = R − 2 H v 2 = R + 2 H v 1 = R v (2) v 1 {v}_1 v 1 v 2 v_2 v 2
ω = 2 ( v 1 − v 2 ) H \begin{equation}
\omega = \frac{{2({v_1} - {v_2})}}{H}
\end{equation} ω = H 2 ( v 1 − v 2 ) 因此,两轮差速驱动模型的正向运动学为:
{ ω = v 1 − v 2 H v = ω ∗ R = v 1 + v 2 2 R = H ( v 1 + v 2 ) 2 ( v 1 − v 2 ) \begin{equation}
\left\{ \begin{array}{l}
\omega = \frac{{{v_1} - {v_2}}}{H}\\
v = \omega *R = \frac{{{v_1} + {v_2}}}{2}\\
R = \frac{{H({v_1} + {v_2})}}{{2({v_1} - {v_2})}}
\end{array} \right.
\end{equation} ⎩ ⎨ ⎧ ω = H v 1 − v 2 v = ω ∗ R = 2 v 1 + v 2 R = 2 ( v 1 − v 2 ) H ( v 1 + v 2 ) 可以使用PD控制进行简单的转向控制。根据期望航向角速与状态观测器得到的反馈航向角速的误差经过PD控制器得到驱动轮的力矩输出,将输出相反地叠加到纵向运动控制得到的驱动轮力矩控制量中,即可实现转向控制。
为了使腿的长度变化具有类似弹簧的阻尼特性,使用PD控制进行腿长控制。因为轮足机器人的腿部主要承受的是机器人的机体重量,因此可以在PD控制中加入前馈控制,补偿机体的重力。
轮足机器人的主要重量都在机器人的机体上,因此在转弯时,较高的重心会使机器人向外倾斜,表现为机体的横滚角会出现一定的偏移。单纯的腿长控制并不足以克服这种扰动。为此加入横滚角补偿,将横滚角误差作为PID控制器的输入,乘以一定的比例系数,将补偿输出以相反的符号叠加到腿长控制器的输出中,让机器人在转弯或复杂地形运动时保证机体的水平。
[1] 陈阳, 王洪玺, 张兰勇. 轮腿式平衡机器人控制[J]. 信息与控制, 2023, 52(5): 648-659
[2] 于红英,唐德威,王建宇.平面五杆机构运动学和动力学特性分析[J].哈尔滨工业大学学报,2007(06):940-943.
[3] Jia Q, Cao X, Sun H, et al. A novel design of a two-wheeled robot[C]//2007 2nd IEEE Conference on Industrial Electronics and Applications. IEEE, 2007: 1226-1231.
Last update on : 2025/01/24